Недостатки аналоговых носителей звука вкупе с неумолимым ходом прогресса привели человека к мысли о том, что звук можно представить в виде информации для записи на цифровые носители. Эта же участь не миновала сегодня ни одного объекта, поддающегося количественному и качественному описанию в системе визуальных и звуковых параметров. Каковы же общие принципы превращения аналогового звука в последовательность цифр?

Аналоговый сигнал при помощи АЦП (аналогово-цифрового преобразователя) разбивается на мелкие участки длительностью в несколько стотысячных долей секунды. На каждом из таких участков АЦП производится измерение амплитуды звука. Величина, обратная длине этих участков, называется частотой дискретизации и измеряется, как и частота звука, в герцах. Очевидно, чем она выше (чем чаще мы измеряем амплитуду), тем более полную информацию о сигнале мы сможем сохранить.

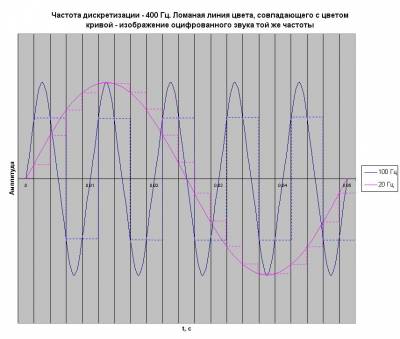
Слишком частые измерения, однако, требуют много места для хранения полученной информации. С другой стороны, уменьшение частоты дискретизации приводит к потере информации, содержащейся в сигнале. Как же выбрать оптимальную частоту дискретизации? Ответ дает известная теорема Котельникова, согласно которой звук с частотой f не может быть оцифрован при частоте дискретизации ниже 2f. Это означает, к примеру, что попытка оцифровки звука частотой, скажем, 1000 Гц при частоте дискретизации 1000 Гц обречена на неудачу. Результатом будет тишина, либо искаженный звук, не имеющий ничего общего с первоначальным. Важным следствием из этой теоремы является установление достаточного верхнего предела значения частоты дискретизации.

Общепринятая верхняя граница частоты звука, воспринимаемого нашим ухом, равна 20 000 Гц. Следовательно, верхний достаточный предел частоты дискретизации звука можно принять за 40 000 Гц. В реальности частота дискретизации при записи звука на CD составляет 44 100 Гц. Профессиональная студийная аппаратура рассчитана на работу со звуком частотой дискретизации 48 000 Гц. Стандарт частоты дискретизации для телефонной линии принят за 8 000 Гц. Этого вполне достаточно для того, чтобы сохранить информацию, содержащуюся в голосовом сообщении, а также сохранить эмоциональную окраску и обеспечить узнаваемость голоса.

На этом история с дискретизацией не оканчивается. Разбивая звуковой сигнал на участки определенной длины и измеряя амплитуду колебаний на этих участках, не стоит забывать, что значение этой амплитуды при записи в память компьютера также может иметь только строго определенные дискретные значения. Это говорит о том, что количество ступенек между максимальным и минимальным значениями амплитуды ограничено. От количества этих ступенек зависит их высота (разница между соседними значениями амплитуды) и, следовательно, чем их больше, тем выше качество звука.

Особенности хранения информации в памяти компьютера привели к количеству возможных ступенек 256, 65536, 16777216 и 4 294 967 296 штук. Этим цифрам соответствуют 8-, 16-, 24- и 32-битный звуки (соответствующие степени числа два, так как компьютер работает с двоичным кодом). Конечно же, повышение «битности» звука ведет к увеличению количества информации. Однако 16-битного звука (65536 вариантов амплитуды звука) обычно вполне достаточно для качественной записи большинства звуковых сигналов.

Теперь мы с легкостью сможем подсчитать, сколько места займет трехминутный стереосигнал при записи на обычном музыкальном компакт-диске. 180 секунд умножаем на 44 100 Гц, затем на 2 байта (это соответствует 16 битам), затем еще на 2 (количество каналов, так как сигнал стереофонический). Итоговая цифра – 31 752 000 байт, или около 30,3 Мбайт информации. Довольно много, правда? Можно ли уменьшить без заметной потери качества? Можно. Но это тема совсем другой статьи.

Источник материала: http://shkolazhizni.ru/archive/0/n-12459/
Автор материала: Сергей

Отправить

Ой! Кажется, вы не можете оставить комментарий. Как это исправить:

Выполнить вход Создать аккаунт